最早是学校的测试题，因为主要负责这部分，所以就顺带总结一下；时隔三年，编码的时候正好发现有相关的需要，所以又加一些内容

逆变换法产生特定分布的随机数

原理

R中所有随机变量的产生都需要通过均匀伪随机数产生器（uniform random number generator）生成。0到1之间的均匀伪随机数可以使用runif(n)函数实现，生成a到b之间的均匀随机数则可通过runif(n, a, b)。通过均匀分布随机数生成任意概率分布随机数的方法称为逆变换法（Inverse Transform method）。

基于概率积分变换定理（Probability Intergral Transformation）

若$X$为（要生成的）连续型随机变量，已知其CDF（Cumulative distribution function）为$F_X$，则

\[U=F_X^{-1}(X) \sim U(0,1)\]

若$X$为离散型随机变量，其可能的取值记为：$\cdots<x_{i-1}<x_{i}<x_{i+1}<\cdots$，进而定义

\[F_{X}^{-1}(u)=\inf \left\{x : F_{X}(x) \geq u\right\}\]

则逆变换为$F_{X}^{-1}(u)=x_{i}$，其中$F_{X}\left(x_{i-1}\right)<u \leq F_{X}\left(x_{i}\right)$ 。

证明

定义：

\[F_{X}^{-1}(u)=\inf \left\{x : F_{X}(x)=u\right\}, \quad 0<u<1\]

那么

\[\begin{aligned} P\left(F_{X}^{-1}(U) \leq x\right) &=P\left(\inf \left\{t : F_{X}(t)=U\right\} \leq x\right) \\ &=P\left(U \leq F_{X}(x)\right)=F_{U}\left(F_{X}(x)\right)=F_{X}(x) \end{aligned}\]

实验准备

R软件，如果在windows有安装scoop的话，可以直接scoop install r
Rstudio，R的IDE，貌似是用chromium实现的一个R的IDE，推荐使用R markdown来跑下面的代码（不然的话，我试过，只能粘贴到命令行才能看到绘图了），使用R Markdown的步骤
1. 在File选项下拉 -> New File -> R Markdown
2. 将代码粘贴到Markdown的代码框部分
3. 代码块的右上角，第三个是运行的图标，点击即可看到实验的绘图

用逆变换法产生Gamma 分布随机数：

\[F(x)=\int_{0}^{x} \frac{\lambda e^{-\lambda y}(\lambda y)^{n-1}}{(n-1) !} d y\]

步骤

Step 1. 产生区间$(0,1)$上的$n$ 个均匀分布随机数$U_1,U_2,\dots,U_n$;

Step 2. 令

\[X=-\frac{1}{\lambda} \log U_{1}-\frac{1}{\lambda} \log U_{2}-\cdots-\frac{1}{\lambda} \log U_{n}=-\frac{1}{\lambda} \log \left(U_{1} U_{2} \cdots U_{n}\right)\]

b.gamma=function(m, n, lambda){
  X=0
  for (i in 1:m) {
    U=runif(n); X[i]=-1/ lambda*sum(log(U))
  }
  X
}
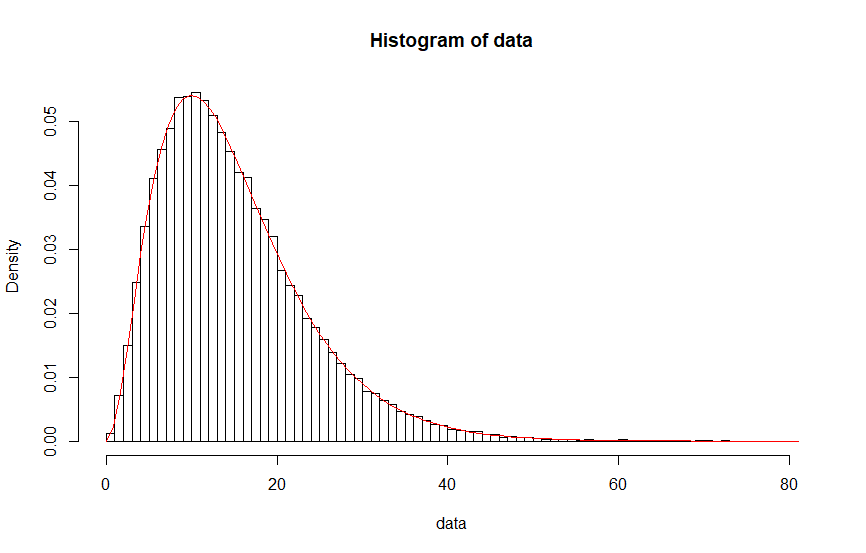
data=b.gamma(100000,3,0.2)
hist(data,prob=TRUE,breaks = 100,main = "Histogram of rGamma")
#hist(rgamma(100,3,0.2))
x = seq(0,max(data),length.out=1000)
curve(dgamma(x,3,0.2), col="red",add=TRUE)

效果还是可以的：

Histogram of rGamma

用逆变换法产生离散型随机变量随机数

在泊松分布分布律给定的情形下，运用R软件，利用逆变换法模拟产生随机数。泊松分布分布律如下：

\[p_{i}=P\{X=i\}=e^{-\lambda} \frac{\lambda^{i}}{i !}, \quad i=0,1, \cdots\]

步骤

Step 1. 产生一个区间$（0,1）$上的均匀分布随机数$U$;

Step 2. 令$i = 0$, $p = e^{-\lambda}$ , $F =p$;

Step 3. 如果$U < F$ ，令$X = i$并停止;

Step 4. $p \leftarrow \lambda p /(i+1), F \leftarrow F+p, i=i+1$

Step 5. 返回Step 3.

b.rpois=function(n,lambda){
  Y=0
  for(j in 1:n) {
    u=runif(1)
    i=0;p=exp(-lambda);F=p
    while (u>=F){
      p=lambda*p/(i+1);
      F=F+p; 
      i=i+1;
    }
    Y[j]=i;
  }
  Y
}
data=b.rpois(100,3)
hist(data,prob=TRUE)

用极坐标变换法(Box-Muller)产生正态分布随机数

正态分布密度函数:

\[f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}\]

原理

当$x$和$y$是两个独立且服从[0,1)均匀分布的随机变量时，$\cos (2\pi x) \cdot \sqrt { - 2\ln (1 - y)}$和$\sin (2\pi x) \cdot \sqrt { - 2\ln (1 - y)} $是两个独立且服从正态分布的随机变量

本质上也是应用了反变换法

把反变换法推广到二维的情况，设$U_1,U_2$为$(0,1)$上的均匀分布随机变量，$(U_1,U_2)$的联合概率密度函数为$f(u_1,u_2)=1(0 \le u_1,u_2 \le 1)$，若有：

\[\left\{\begin{matrix} {U_1} = {g_1}(X,Y)\\ {U_2} = {g_2}(X,Y) \end{matrix}\right.\]

其中，$g_1,g_2$的逆变换存在，记为

\[\left\{\begin{matrix} x = {h_1}({u_1},{u_2})\\ y = {h_2}({u_1},{u_2}) \end{matrix}\right.\]

且存在一阶偏导数，设$J$为Jacobian矩阵的行列式

\[\left | J \right | =\begin{vmatrix} \frac{\partial x}{\partial u_1} & \frac{\partial x}{\partial u_2} \\ \frac{\partial y}{\partial u_1} & \frac{\partial y}{\partial u_2} \end{vmatrix} \ne 0\]

则随机变量$(X,Y)$的二维联合密度为（回顾直角坐标和极坐标变换）：

\[f[h_1(u_1,u_2),h_2(u_1,u_2)] \cdot \left | J \right | = \left | J \right |\]

根据这个定理我们来证明一下，

\[\left\{\begin{matrix} X = \sqrt {- 2\ln U_1} \cos (2\pi U_1) \\ Y = \sqrt {- 2\ln U_1} \sin (2\pi U_2) \end{matrix}\right.\]

求反函数得

\[\left\{\begin{matrix} U_1 = e^{ - \frac{X^2 + Y^2}{2}} \\ U_2 = \frac{1}{2 \pi} \arctan \frac{Y}{X} \end{matrix}\right.\]

计算Jacobian行列式

\[\begin{align} \left | J \right | =\begin{vmatrix} \frac{\partial U_1}{\partial X} & \frac{\partial U_1}{\partial Y} \\ \frac{\partial U_2}{\partial X} & \frac{\partial U_2}{\partial Y} \end{vmatrix} & =-(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}X^2})(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}Y^2}) \end{align}\]

由于$X_1,X_2$为$(0,1)$上的均匀分布，概率密度函数均为$1$，所以$X,Y$的联合概率密度函数为

\[-(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}X^2})(\frac{1}{\sqrt{2 \pi}}e^{-\frac{1}{2}Y^2})\]

所以$Y_1,Y_2$是两个独立且服从正态分布的随机变量

步骤

Step 1. 产生区间$(0, 1)$ 上的均匀分布随机数$U_1,U_2$

Step 2. 令$R^{2}=-2 \log \left(U_{1}\right), \quad \theta=2 \pi U_{2}$

Step 3. 令

\[X=R \cos \theta=\sqrt{-2 \log \left(U_{1}\right)} \cos \left(2 \pi U_{2}\right)\] \[Y=R \sin \theta=\sqrt{-2 \log \left(U_{1}\right)} \sin \left(2 \pi U_{2}\right)\]

b.rnorm=function(n){
  X=0; Y=0
  for (i in 1:n) {
    U1=runif(1); U2=runif(1)
    X[i] <- sqrt(-2*log(U1))*cos(2*pi*U2)
    Y[i] <- sqrt(-2*log(U1))*sin(2*pi*U2)
  }
  c(X, Y)
}

hist(b.rnorm(1000),prob=TRUE)
curve(dnorm, col="red",add=TRUE)

均匀分布随机数相加产生近似正态分布的随机数

当时看到代码中使用均匀分布随机数相加产生近似正态分布的随机数的时候，再次翻了下逆变换法的原理以及正态分布的导出，但是反解$F_X^{-1}(X)$是怎么也想不通，所以就搜索了下”multiple uniform random add normal”，看到一篇博文：Sums of uniform random values 提到了

method for generating a standard normal: add 12 uniform random variables and subtract 6.

这个正是我在代码中看到的方法，这个确实很巧妙，免去了繁琐的方式实现正态分布的随机数的生成；上文并未提到这个是什么原因，也没有给精度相关的证明，但是给出了PDF的表达式（后文的wiki的PDF应该才是对的）

看不出来和正态分布的关系，我尝试了统计实验

b.rutonorm=function(n,lambda){
  Y=0
  for(j in 1:n) {
    i=0
    for(k in 1:lambda){
      u=runif(1)
      i=i+u;
    }
    Y[j]=i;
  }
  Y
}
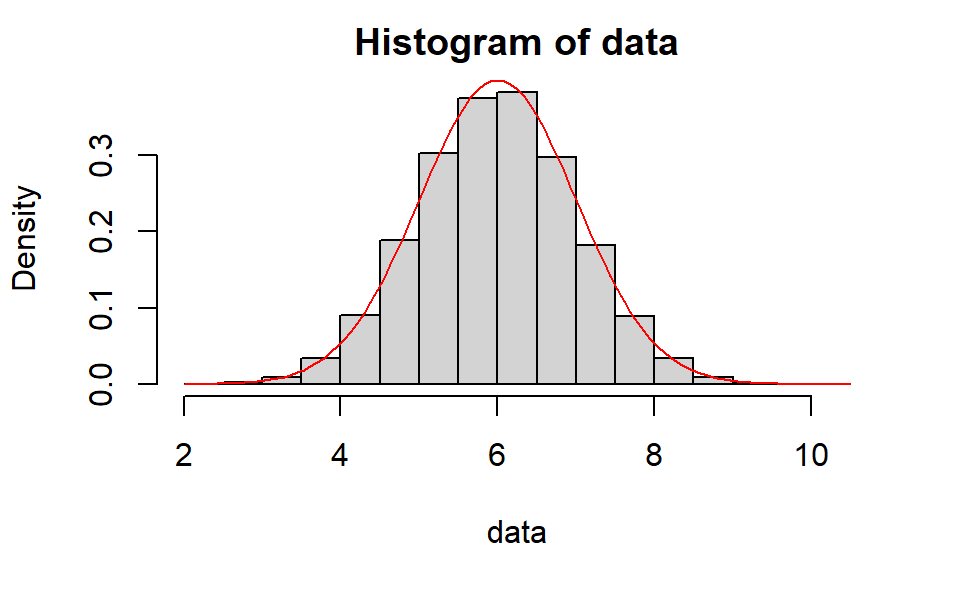
lambda=12
data=b.rutonorm(100000,lambda)
hist(data,prob=TRUE)
curve(dnorm(x,mean=6,sd=1), col="red",add=TRUE)

近似的效果看起来很好

接着可以搜索到维基百科的词条：Irwin–Hall distribution，总算是看到了PDF:

\[{\displaystyle f_{X}(x;n)={\frac {1}{2(n-1)!}}\sum _{k=0}^{n}(-1)^{k}{n \choose k}(x-k)_{+}^{n-1}}\]

近似正态分布： ${\displaystyle \phi (x)={\mathcal {N}}(\mu,\sigma ^{2})}$ 其中：

\[{\displaystyle \mu =n/2}, {\displaystyle \sigma ^{2}=n/12}\]

PREVIOUS配置Windows下的终端与Shell

NEXT家用宽带的IPv6配置